Addition is the most fundamental operation for any computer. From crunching numbers (their original purpose) to rendering advanced graphics, everything a computer needs to do depends on adding quickly and accurately. 
 
Forget base-10, keyboards, and even screens. The earliest computers didn’t have any of that. Switches and relays are all that a computer needs to add numbers. 
 
The tools available to these early programmers were the NOT gate (turns 0 to 1, 1 to 0; also known as the inverter), AND gate (outputs 1 if both inputs are 1), and OR gate (outputs 1 if at least one input is 1). There are two more gates, the NAND and NOR, made from placing an inverter at the outputs of their respective gates. 
 
To deconstruct this problem, we can first consider the simplest adding machine: taking two one-bit inputs and then outputting their sum. The chart below shows the results for all possible sums. 
 

S	0	1
0	00	01
1	01	11

As you can see, this addition gives a two-bit result: the sum and the carry. We first look at the carry bit: 
 

C	0	1
0	0	0
1	0	1

Notice how the carry is only 1 when bit 1 AND 2 are both 1. This matches the behaviour of the AND gate. 
 
The sum bit is harder to deal with: if exactly one input is 1, the sum will be 1, but if both are one, the sum is 0 as the result is carried.

 

S	0	1
0	0	1
1	1	0

 
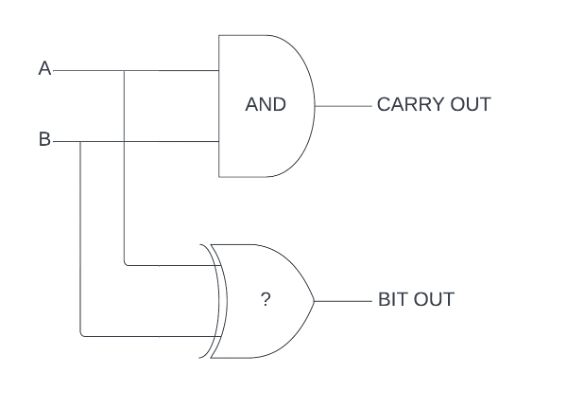
This type of decision is more complicated than the first. How do we program this with the gates we have? 
 
Looking at the available gates, the OR and NAND (AND with output reversed) both give results close to the ones we want: 
 

OR	0	1
0	0	1
1	1	1

 
 

NAND	0	1
0	1	1
1	1	0

 
 
If we connect the inputs to both gates and compare their outputs with an AND gate, we get the output we need. 
 

 
 
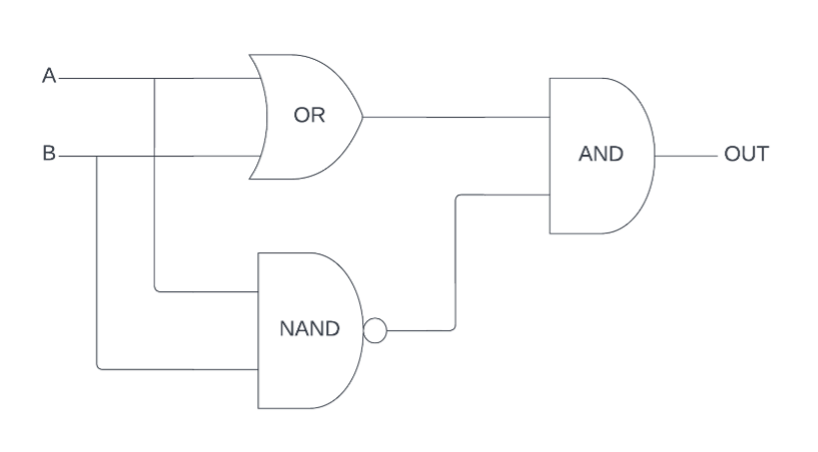
This is the exclusive-or gate, or XOR for short. With this, we can compute the sum and carry by connecting the inputs to an AND and XOR gate respectively.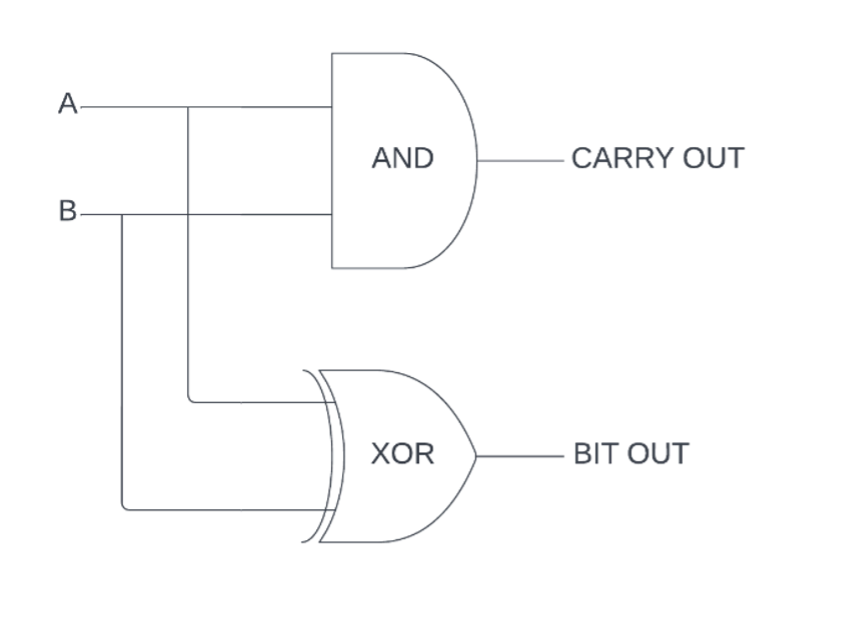 

 
This arrangement is known as a half adder. As you might have guessed, it is so called because it is incomplete: to work properly in a chain, an adder needs to take the carry from the previous adder into account. 
 
If two half adders and an OR gate are chained together (properly, a XOR gate would be required, though as the inputs to it cannot both be 1, an OR gate is sufficient), the carry can be added with the other two inputs, making the full adder. 
 

 
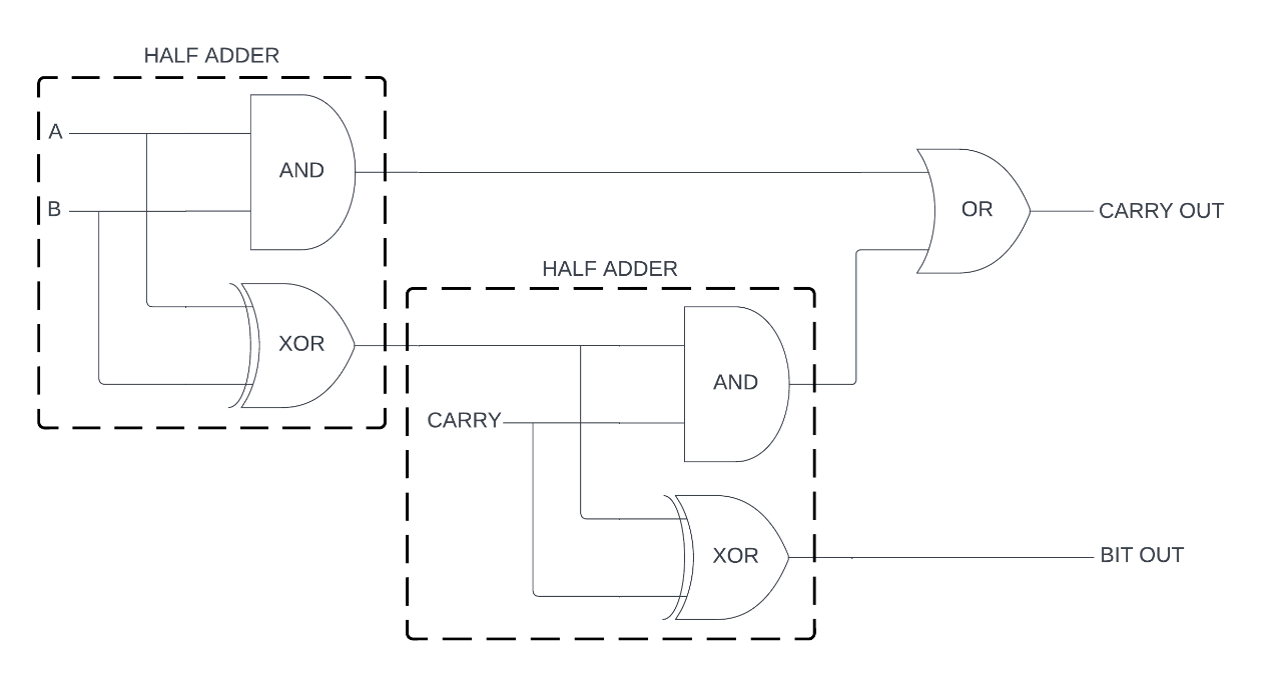
The full adder can be chained as many times as needed to add together binary numbers. Of course, there are techniques for speeding up long chains of adders, and storing their results is another problem with a basic adder array connected to, say, a series of lightbulbs. However, this is essentially what is needed to add numbers together, using nothing but logic and some electrical currents.